На брусок массой 1 кг который неподвижно лежал на горизонтальном столе

Обновлено: 28.04.2024

Тип 30 № 25710

К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.

Какие законы Вы используете для описания движения бруска? Обоснуйте их применение.

Обоснование. Движение бруска поступательное. Следовательно, его можно считать материальной точкой. При движении бруска по горизонтальной поверхности на него действуют силы тяжести, упругости, трения и реакции опоры. Систему отсчета, связанную с неподвижной плоскостью, можем считать инерциальной. Поэтому применим второй закон Ньютона.

Так как поверхность горизонтальна, то потенциальная энергия гравитационного взаимодействия бруска и Земли не меняется. На брусок действует внешняя сила трения, поэтому можно применить закон сохранения энергии для незамкнутой системы «брусок — пружина».

Перейдем к решению.

1. Начальная энергия системы равна потенциальной энергии растянутой пружины: После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину Тогда конечная энергия системы равна потенциальной энергии сжатой пружины: Изменение полной энергии системы равно работе силы трения F_тр:

где N — модуль силы реакции опоры.

2. В момент, когда груз остановился, по второму закону Ньютона равнодействующая всех сил стала равна нулю. Пружина сжата, поэтому сила упругости пружины направлена вправо. Её уравновешивает сила трения покоя, которая направлена против возможного движения, причём эта сила максимальна, т. к. по условию начальное положение пружины соответствует максимальному растяжению пружины, при котором груз движется таким образом.

Запишем закон Ньютона для горизонтальной и вертикальной осей:

3. Подставим полученное выражение для x в равенство из пункта 1:

После подстановки получим

Тип 30 № 25711

К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён груз массой m = 1 кг, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите коэффициент трения груза по плоскости.

Приращение полной энергии системы равно работе силы трения

Запишем закон Ньютона для вертикальной и горизонтальной оси:

Тип 30 № 25712

К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён груз массой m = 1 кг, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости Груз смещают по горизонтали, растягивая пружину на величину d, затем отпускают с начальной скоростью, равной нулю. Найдите максимальное значение d, при котором груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата.

Тип 6 № 8857

К железному бруску массой 7,8 кг привязали тонкую невесомую нерастяжимую нить, которую перекинули через неподвижный идеальный блок, а сам брусок целиком погрузили в воду (см. рис.). Свободный конец нити удерживают, действуя на него с некоторой силой так, что брусок находится в равновесии. Установите соответствие между физическими величинами и их численными значениями, выраженными в указанных единицах. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

А) модуль силы натяжения нити, Н

Б) объём бруска, дм 3

Зная массу железного бруска, можем найти его объем:

Запишем второй закон Ньютона для бруска:

Найдем отсюда модуль силы натяжения нити:

Тип 6 № 8899

К алюминиевому бруску массой 5,4 кг привязали тонкую невесомую нерастяжимую нить, которую перекинули через неподвижный идеальный блок, а сам брусок целиком погрузили в воду (см. рис.). Свободный конец нити удерживают, действуя на него с некоторой силой так, что брусок находится в равновесии. Установите соответствие между физическими величинами и их численными значениями, выраженными в указанных единицах. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Зная массу алюминиевого бруска, можем найти его объем:

Аналоги к заданию № 8857: 8899 Все

Тип 30 № 25936

Маленький шарик массой подвешен на лёгкой нерастяжимой нити длиной которая разрывается при силе натяжения Шарик отведён от положения равновесия (оно показано на рисунке пунктиром) и отпущен. Когда шарик проходит положение равновесия, нить обрывается, и шарик тут же абсолютно неупруго сталкивается с бруском массой лежащим неподвижно на гладкой горизонтальной поверхности стола. Какова скорость u бруска после удара? Считать, что брусок после удара движется поступательно.

Какие законы Вы используете для описания взаимодействия тел? Обоснуйте их применение к данному случаю.

Обоснование. Шарик и брусок в данных условиях можно считать материальными точками. При отсутствии силы сопротивления воздуха и трения в инерциальной системе отсчета для шарика и бруска применим закон сохранения импульса при абсолютно неупругом ударе. Внешняя сила тяжести действует в течение очень малого промежутка времени взаимодействия, поэтому этим действием можно пренебречь.

Нить невесома и нерастяжима, на шарик действуют сила тяжести и сила натяжения нити.

Равнодействующая сил в момент удара является причиной возникновения центростремительного ускорения для равномерного движения по окружности. Можем применять для инерциальной системы отсчета второй закон Ньютона.

Перейдем к решению. 1. Непосредственно перед обрывом нити в момент прохождения положения равновесия шарик движется по окружности радиусом l со скоростью В этот момент действующие на шарик сила тяжести и сила натяжения нити направлены по вертикали и вызывают центростремительное ускорение шарика (см. рис.). Запишем второй закон Ньютона в проекциях на ось Oy инерциальной системы отсчёта Oxy, связанной с Землёй:

2. При прохождении положения равновесия нить обрывается, и шарик, движущийся горизонтально со скоростью абсолютно неупруго сталкивается с покоящимся бруском. При столкновении сохраняется импульс системы шарик — брусок. В проекциях на ось Ox получаем:

где u — проекция скорости бруска с шариком после удара на эту ось. Отсюда:

На брусок массой 1 кг который неподвижно лежал на горизонтальном столе

Тип 30 № 29763

На горизонтальном столе лежит брусок массой кг, к нему через легкий неподвижный блок привязан груз массой Груз начинают тянуть с силой под углом к горизонту (см. рис.). Определите скорость груза в момент достижения им высоты поверхности стола, если первоначально груз находился на расстоянии 32 см от поверхности стола. Коэффициент трения равен 0,3. Обоснуйте применимость используемых законов к решению задачи.

Обоснование.

Рассмотрим движение бруска и груза относительно Земли, которая является инерциальной системой отсчета. На брусок действуют силы: приложенная сила F, сила тяжести Mg, сила трения сила реакции опоры N и сила натяжения нити T₁. Движение бруска прямолинейное равноускоренное с ускорением a₂. На груз действуют сила тяжести mg и сила натяжения нити T₂, под действием которых груз движется прямолинейно и равноускорено с ускорением a₂. Так как движение этих тел поступательное, то его можно описывать моделью материальной точки. По условию нить невесома и нерастяжима, поэтому ускорения тел и силы натяжения нити равны модулю. Тогда можно считать, что В инерциальной системе отсчета можем применить второй закон Ньютона.

1. Запишем второй закон Ньютона для бруска и груза:

Найдем проекции уравнений на координатные оси:

Учтем, что сила трения скольжения равна

2. Грузик двигался из состояния покоя равноускорено. Тогда откуда

3. Объединив все уравнения, найдем скорость груза при подъеме на высоту 32 см, получим

В обосновании возможности использования законов (закономерностей) допущена ошибка.

Приведено полное решение, включающее следующие элементы:

I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом;

II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов);

III) представлены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);

Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеется один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.

В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты.

В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.

Представлены записи, соответствующие одному из следующих случаев.

Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Источник: ЕГЭ по физике 06.06.2022. Основная волна. Разные задачи, ЕГЭ по физике 06.06.2022. Основная волна. Свердловская область

Чивилев В. Закон сохранения импульса // Квант

Чивилев В. Закон сохранения импульса // Квант. — 2000. — № 2. — С. 30-31, 34.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Импульсом материальной точки называется произведение массы точки на ее скорость: . Импульсом системы материальных точек называется векторная сумма импульсов отдельных точек: . Любое макроскопическое тело или несколько макроскопических тел можно рассматривать как систему материальных точек, поскольку каждое тело можно мысленно разбить на сколь угодно малые части и считать их материальными точками. В дальнейшем систему материальных точек для краткости будем называть просто системой.

Из законов Ньютона следует, что в инерциальной системе отсчета справедливо векторное равенство

где — сумма всех внешних сил, действующих на систему в течение сколь угодно малого интервала времени Δt (Δt > 0), а — изменение импульса системы за это время. Произведение называется импульсом силы. Обратите внимание, что — это сумма только внешних сил, т.е. сил, действующих на тела системы со стороны тел, не входящих в систему. Внутренние силы, т.е. силы взаимодействия между частями системы, в равенство (1) не входят.

Если в течение времени Δt (Δt > 0) сумма внешних сил равна нулю, т.е. , то и , т.е. импульс системы в течение Δt сохраняется. Когда время взаимодействия тел системы (время опыта) не мало, его можно разбить на сколь угодно малые интервалы: , где k = 1, 2, 3 . Если в течение каждого такого интервала сумма внешних сил равна нулю, то импульс системы будет сохраняться в течение этого интервала и, как следствие, в течение всего времени опыта. Напомним, что замкнутой (изолированной) системой называется система, тела которой не взаимодействуют с другими телами (внешним миром). Ясно, что для замкнутой системы и .

Итак, в инерциальной системе отсчета импульс системы материальных точек сохраняется в течение некоторого времени Δt (не обязательно малого) в двух случаях:

1) система в течение Δt замкнута (изолирована);

2) система не замкнута, т.е. внешние силы есть, но их сумма равна нулю в течение всего времени Δt.

Это утверждение и представляет собой закон сохранения импульса в развернутой формулировке.

Импульс системы — это вектор, и его сохранение в течение некоторого времени взаимодействия частей системы встречается не так часто, хотя бы потому, что в земных условиях строго замкнутой системы нет в принципе из-за наличия внешней силы — силы притяжения к Земле. Да и равенство нулю суммы всех внешних сил на протяжении некоторого интервала времени может реализоваться только при вполне определенных условиях. Гораздо чаще встречается случай, когда за время Δt векторная сумма внешних сил не равна нулю, но равна нулю сумма их проекций на некоторую ось X в пространстве. Тогда в течение этого времени сохраняется проекция на ось X импульса системы. Действительно, запишем равенство (1) в проекциях на ось Х:

где F_x — проекция на ось X суммы всех внешних сил (по правилам действия с векторами F_x равна сумме проекций на ось X всех внешних сил), а Δр_х — проекция на ось X изменения импульса системы (по правилам действия с векторами Δр_х равна изменению проекции на ось X импульса системы). Если в течение времени то из равенства (2) следует, что и . Если же время Δt опыта не мало, то после разбиения его на сколь угодно малые интервалы легко показать, что при выполнении в течение произвольного Δt условия будет иметь место следствие .

Иными словами, в инерциальной системе отсчета проекция на некоторую ось X импульса системы материальных точек сохраняется в течение некоторого времени Δt (не обязательно малого), если сумма проекций на ось X всех внешних сил, действующих на систему, равна нулю в течение этого времени Δt.

На основании этого утверждения о сохранении проекции импульса и решается большинство задач. При этом часто запись уравнения, отражающего сохранение проекции импульса в виде равенства начальной и конечной проекций импульса, обосновывается фразой «по закону сохранения импульса», что не совсем точно. Но поскольку эта неточность не влияет на результат при решении задачи, на нее, как правило, никто не обращает внимания, в том числе и экзаменаторы.

Скажем несколько слов о приближенном сохранении импульса или его проекции. Равенство (1) тем точнее, чем меньше Δt. Конечное время опыта Δt можно разбить на сколь угодно малые интервалы времени Δt_k и записать для каждого из них равенство

Сложив все такие равенства, получим новое, внешне похожее на (1):

где — некоторая средняя внешняя сила, действующая в течение Δt и определяемая из равенства , а — изменение импульса системы за конечное время Δt. Аналогично получается и внешне похожее на (2) равенство в проекциях:

где F_x _cp — некоторое среднее значение суммы проекций на ось X всех внешних сил в течение конечного времени опыта Δt, а Δр_х — изменение проекции на ось X импульса системы за это время. Ясно, что при (например, в любой момент опыта) из равенства (3) следует и . При из равенства (4) следует . Если же в течение времени опыта не выполняется строго или , то за «помощью» в решении задачи следует обращаться к равенствам (3) и (4) и анализировать их. Иногда можно считать, что величины F_cp·Δt или F_x _cp·Δt, характеризующие импульс силы, малы. Тогда из (3) или (4) следует, что или . Такая ситуация встречается при некоторых взаимодействиях тел системы — таких, как удары, когда Δt мало, a F_cp или F_x _cp ограничены из-за ограниченности значений F или F_x в течение опыта.

Теперь рассмотрим несколько конкретных задач. Все они в разные годы предлагались на вступительных экзаменах в Московский физико-технический институт (МФТИ). Автор всех разобранных задач, включая и задачи для упражнений, — автор этой статьи.

Задача 1. После разрыва неподвижного снаряда образовалось четыре осколка. Осколок массой m₁ = 4 кг полетел вертикально вниз со скоростью υ₁ = 150 м/с, осколок массой m₂ = 3 кг полетел горизонтально на юг со скоростью υ₂ = 100 м/с, осколок массой m₃ = 1 кг — горизонтально на восток. Осколок массой m₄ = 3,5 кг полетел со скоростью υ₄ = 200 м/с. Найдите скорость осколка массой m₃.

Рассмотрим систему из четырех осколков. За малое время разрыва Δt действием внешних сил — сил тяжести — можно пренебречь, поскольку за то время они не вызывают существенного изменения импульса осколков из-за их малости по сравнению с внутренними силами, действующими между осколками. Поэтому можно считать, что импульс системы сохраняется (приближенно):

Длина вектора равна длине диагонали АВ прямоугольного параллелепипеда, построенного на векторах и (рис. 1). Следовательно,

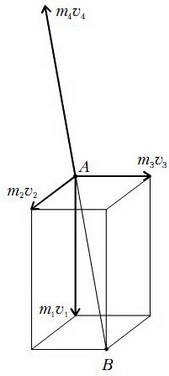
Из последнего равенства находим

Задача 2. Между шариками с массами m и М, связанными нитью, вставлена легкая пружина жесткостью k, сжатая на некоторую величину (рис.2). Система движется со скоростью υ₀ вдоль прямой, проходящей через центры шариков. Нить пережигают, и один из шариков останавливается. Найдите начальную величину сжатия пружины.

Система из шариков, пружины и нити предполагается замкнутой.

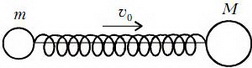
В земных условиях смоделировать процесс, описанный в задаче, можно на гладком горизонтальном столе. Ясно, что остановиться может только левый шарик, так как пружина на него действует силой, направленной против его начальной скорости. Пусть скорость правого шарика после распрямления пружины равна . По закону сохранения импульса,

Заметим, что совпадение направлений скоростей и следует именно из последнего равенства. Взяв модули от левой и правой частей этого равенства (точнее, записав равенство в проекциях на ось X, направленную вдоль оси пружины), получим

По закону сохранения энергии,

Исключая из последних двух уравнений υ, находим искомую величину сжатия пружины

Задача 3. Кусок пластилина массой m = 32 г попадает в брусок массой 6m, двигавшийся по гладкой горизонтальной поверхности стола (рис. 3), прилипает к бруску и далее движется с ним по столу. Перед ударом скорость куска пластилина равна υ = 7 м/с и направлена под углом α = 60° к горизонту, а скорость бруска равна υ/4 и лежит в одной вертикальной плоскости со скоростью пластилина. Определите скорость бруска с пластилином после удара. На сколько увеличилась суммарная внутренняя энергия бруска, пластилина и окружающих тел?

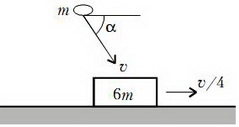
Внешние силы, действующие на систему из бруска и пластилина за время их взаимодействия Δt, — это силы тяжести и 6 и зависящая от времени сила нормальной реакции стола на брусок, направленная вертикально вверх. Ясно, что сумма внешних сил

в произвольный момент интервала времени Δt не равна нулю. Этим и объясняется, что импульс системы не сохраняется. Впрочем, несохранение импульса сразу бросается в глаза — начальный суммарный импульс системы направлен вправо и вниз, а конечный — вправо и горизонтально.

Если импульс системы не сохраняется, то следует поискать ось в пространстве, для которой сохраняется проекция импульса системы. Поэтому проанализируем выражение для . Ясно, что для горизонтальной оси X, направленной вдоль начальной скорости бруска, в любой момент из интервала Δt, поэтому проекция на ось X импульса системы сохраняется:

откуда и находим скорость бруска с пластилином:

Величину ΔW увеличения внутренней энергии бруска, пластилина и окружающих тел найдем из закона сохранения и превращения энергии:

откуда, с учетом выражения для u, получаем

Задача 4. Пуля летит горизонтально со скоростью υ₀, пробивает лежащую на горизонтальной поверхности стола небольшую коробку и вылетает в том же направлении с втрое меньшей скоростью. Масса коробки в 5 раз больше массы пули. Коэффициент трения скольжения между коробкой и столом μ. Найдите скорость коробки сразу после вылета из нее пули. На какое расстояние передвинется при этом коробка?

Рассмотрим систему из коробки и пули. Пусть масса пули m, масса коробки 5m, скорость коробки сразу после вылета пули υ. За время взаимодействия Δt (пролета пули через коробку) на систему действуют такие внешние силы: направленные вертикально вниз силы тяжести и 5, направленная вертикально верх и мало изменяющаяся со временем сила нормальной реакции стола и направленная против скорости коробки сила трения со стороны стола (рис. 4).

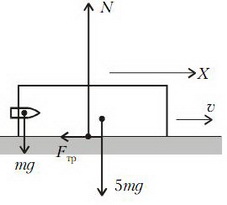
Ясно, что сумма внешних сил в течение Δt не равна нулю. Не равна нулю и проекция F_x на горизонтальную ось X, направленную вдоль скорости коробки: . Но действием ограниченной по величине силы трения за малое время пролета Δt можно пренебречь и считать, что . Тогда за время пролета пули проекция на ось X импульса системы сохраняется (приближенно):

откуда и находим скорость коробки:

После вылета пули скорость коробки с течением времени уменьшается под действием силы трения, равной 5μ·m·g. Расстояние s, на которое передвинется коробка, найдем из закона сохранения и превращения энергии:

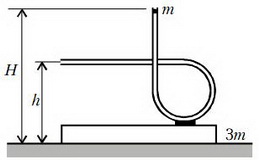
Задача 5. Трубка в форме петли укреплена на бруске, находящемся на гладкой горизонтальной поверхности стола (рис. 5). Нижний конец трубки горизонтален и находится на расстоянии h от стола. Шарик массой m, который может скользить по трубке без трения, удерживается на высоте Н от стола. Масса платформы с трубкой 3m. Вначале система покоилась. Шарик отпустили. Найдите скорость вылетевшего из трубки шарика, если: 1) брусок закреплен на столе; 2) брусок не закреплен и после вылета шарика движется поступательно.

1) В случае закрепленного бруска скорость υ₁ вылетевшего шарика найдем из закона сохранения и превращения энергии:

2) В случае незакрепленного бруска будем рассуждать так. Пусть шарик вылетел из трубки со скоростью υ₂, a брусок с трубкой приобрел скорость u в противоположном направлении. На систему из шарика и бруска с трубкой за время Δt движения шарика в трубке действуют такие внешние силы: направленные вертикально вниз силы тяжести и 3 и направленная вертикально вверх и зависящая от времени сила нормальной реакции стола . Заметим, что Δt здесь не считается малым! Направим ось X горизонтально в направлении скорости вылетевшего шарика. Ясно, что проекция на ось суммы всех трех вертикальных сил равна нулю в любой момент из интервала времени Δt. Значит, проекция на ось X импульса системы сохраняется:

По закону сохранения и превращения энергии,

Из последних двух уравнений находим скорость шарика:

1. Неподвижный снаряд разорвался на четыре осколка. Осколки массами m₁ = 3 кг, m₂ = 2 кг и m₃ = 4 кг полетели, соответственно, со скоростями υ₁ = 200 м/с вертикально вверх, υ₂ = 150 м/с горизонтально на север и υ₃ = 100 м/с горизонтально на восток. Под каким углом к горизонту полетел четвертый оcколок?

2. Камень массой m = 1 кг подняли на некоторую высоту и отпустили без начальной скорости. Через время t = 1 с практически свободного падения камень попал в ящик с песком массой 5m, скользивший по гладкой горизонтальной поверхности со скоростью υ = 6 м/с. Найдите скорость ящика с камнем. На сколько увеличилась суммарная внутренняя энергия ящика, песка, камня и окружающих тел?

3. Трубка в виде петли жестко укреплена на платформе, находящейся на гладкой горизонтальной поверхности стола (рис. 6). Правый конец трубки горизонтален, его расстояние до стола h. В трубке на высоте Н удерживается шарик массой m, который может скользить по трубке без трения. Масса платформы с трубкой Δm. Система покоится. Шарик отпускают. Найдите скорость вылетевшего из трубки шарика, если: 1) платформа закреплена на столе; 2) платформа не закреплена и после вылета шарика движется поступательно.

Читайте также: