Мебельная фабрика выпускает столы стулья кресла и кровати

Обновлено: 17.05.2024

– «Формализованные методы принятия решений» – Решение задач принятия решений модифицированным симплексным методом
Мебельная фабрика выпускает диваны, кресла, стулья и столы. Информация о производстве представлена в таблице.
При принятии решения об объемах производства продукции необходимо учесть следующие условия: 1)объем производства кресел должен быть в два раза больше, чем диванов, 2)объем производства стульев должен быть не более, чем в четыре раза больше, чем столов, 3)объем производства столов должен быть не меньше, чем диванов. Требуется определить наилучшую структуру производства, которая обеспечит максимальную массу прибыли. Решить задачу модифицированным симплексным методом.
Показатели Изделия Наличие ресурсов

Диваны Кресла Стулья Столы
Прибыль, руб. 880 360 120 200 –
Древесные плиты, м. кв. 4 2 0,5 1 700
Затраты труда, чел.-ч. 13 8 2 3 2500
Металлические трубки, м
10 3 2 3 1200

Часть выполненной работы

EQ B5,6,7,2,10,8 = bbc| (a al co6 hs6 (1;0;0;2;0;0;0;1;0;8;0;0;0;0;1;3;0;0;0;0;0;1;0;0;0;0;0;0;1;0;0;0;0;0;0;1))
Матрица c.
c = (2, -1, -1, 4, 0, 0, 0, 0, 0, 0)
1. Проверка критерия оптимальности.
Вектор С содержит отрицательные элементы. Поэтому текущий план неоптимален.
Формируем из матрицы С две матрицы: cB – составленная из базисных компонентов вектора С и cN – составленная из небазисных компонентов вектора С.
cB(5,6,7,2,10,8) = (0, 0, 0, -1, 0, 0)
cN(1,3,4,9) = (2, -1, 4, 0)
2. Определение новой базисной переменной.
Матрица N формируется из матрицы А из соответствующих столбцов с номерами N.
Матрица N(1,3,4,9).
4 0.5 1 0
13 2 3 0
10 2 3 0
-2 0 0 1
0 1 -4 0
1 0 -1 0
Вычисляем:
B-1 =
1 0 0 -2 0 0
0 1 0 -8 0 0
0 0 1 -3 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
Умножаем вектор cB на обратную матрицу B-1. Получаем вектор цен u.
u = cBB-1 = (0, 0, 0, -1, 0, 0)
Умножаем обратную матрицу B-1 на вектор b.
EQ b*5,6,7,2,10,8 = B-1 b = bbc| (a al co1 hs6 (700;2500;1200;0;0;0))
Умножаем вектор u на матрицу N: uN = (2, 0, 0, -1)
Тогда вектор нулевой строки c* будет равен разности двух векторов cN и uN:
c*1,3,4,9 = cN – uN = (0, -1, 4, 1)
Откуда номер направляющего столбца s = 2 (индекс максимального по модулю значения из отрицательных элементов).
Выбираем из матрицы А столбец под номером 2.
EQ (a12 … am2) = bbc| (a al co1 hs6 (0,5;2;2;0;1;0))
3. Определение новой свободной переменной.
Умножаем обратную матрицу B-1 на вектор (a12,…,am2)
a* = B-1 (a12,…,am2)T = (0.5, 0, 0, 0, 0, 0)T
min(700:0.5 = 1400;2500:2 = 1250;1200:2 = 600;-;0:1 = 0;-;) = 0
Откуда номер направляющей строки r = 5 (индекс минимального значения).
Итерация №3.
Базисные переменные: = (5, 6, 7, 2, 3, 8)
Выбираем столбцы под номерами (5, 6, 7, 2, 3, 8) из матрицы А и формируем матрицу В.
EQ B5,6,7,2,3,8 = bbc| (a al co6 hs6 (1;0;0;2;0,5;0;0;1;0;8;2;0;0;0;1;3;2;0;0;0;0;1;0;0;0;0;0;0;1;0;0;0;0;0;0;1))
Матрица c.
c = (0, 0, -1, 4, 0, 0, 0, 0, 1, 0)
1. Проверка критерия оптимальности.
Вектор С содержит отрицательные элементы. Поэтому текущий план неоптимален.
Формируем из матрицы С две матрицы: cB – составленная из базисных компонентов вектора С и cN – составленная из небазисных компонентов вектора С.
cB(5,6,7,2,3,8) = (0, 0, 0, 0, -1, 0)
cN(1,4,9,10) = (0, 4, 1, 0)
2. Определение новой базисной переменной.
Матрица N формируется из матрицы А из соответствующих столбцов с номерами N.
Матрица N(1,4,9,10).
4 1 0 0
13 3 0 0
10 3 0 0
-2 0 1 0
0 -4 0 1
1 -1 0 0
Вычисляем:
B-1 =
1 0 0 -2 -0.5 0
0 1 0 -8 -2 0
0 0 1 -3 -2 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
Умножаем вектор cB на обратную матрицу B-1. Получаем вектор цен u.
u = cBB-1 = (0, 0, 0, 0, -1, 0)
Умножаем обратную матрицу B-1 на вектор b.
EQ b*5,6,7,2,3,8 = B-1 b = bbc| (a al co1 hs6 (700;2500;1200;0;0;0))
Умножаем вектор u на матрицу N: uN = (0, 4, 0, -1)
Тогда вектор нулевой строки c* будет равен разности двух векторов cN и uN:
c*1,4,9,10 = cN – uN = (0, 0, 1, 1)
Вектор С не содержит отрицательных элементов. Первый этап симплекс-метода завершен.
Второй этап. Удаляем столбцы с искусственными переменными. Заменим вектор оценок С на целевую функцию.
Выразим базисные переменные:
x2 = 0-2×1
x3 = 0-4×4
которые подставим в целевую функцию:
F(X) = 880×1 + 360(0-2×1) + 120(0-4×4) + 200×4
или
F(X) = 0+1600×1+680×4
Имеем:
Матрица коэффициентов A = aij
4 2 0.5 1 1 0 0 0
13 8 2 3 0 1 0 0
10 3 2 3 0 0 1 0
-2 1 0 0 0 0 0 0
0 0 1 -4 0 0 0 0
1 0 0 -1 0 0 0 1
Матрица b.
EQ b = bbc| (a al co1 hs6 (700;2500;1200;0;0;0))
Итерация №1.
Базисные переменные: = (5, 6, 7, 2, 3, 8)
Выбираем столбцы под номерами (5, 6, 7, 2, 3, 8) из матрицы А и формируем матрицу В.
EQ B5,6,7,2,3,8 = bbc| (a al co6 hs6 (1;0;0;2;0,5;0;0;1;0;8;2;0;0;0;1;3;2;0;0;0;0;1;0;0;0;0;0;0;1;0;0;0;0;0;0;1))
Матрица c.
c = (-1600, 0, 0, -680, 0, 0, 0, 0)
1. Проверка критерия оптимальности.
Вектор С содержит отрицательные элементы. Поэтому текущий план неоптимален.
Формируем из матрицы С две матрицы: cB – составленная из базисных компонентов вектора С и cN – составленная из небазисных компонентов вектора С.
cB(5,6,7,2,3,8) = (0, 0, 0, 0, 0, 0)
cN(1,4) = (-1600, -680, 0, 0)
2. Определение новой базисной переменной.
Матрица N формируется из матрицы А из соответствующих столбцов с номерами N.
Матрица N(1,4).
4 1
13 3
10 3
-2 0
0 -4
1 -1
Вычисляем:
Матрицу B-1 вычисляем чере…

Лекция 13

Мебельная фабрика выпускает столы, стулья, бюро и книжные шкафы. При изготовлении товаров используются два вида досок. В наличии 1500 п.м. досок первого типа и 1000 п.м. второго типа. Трудовые ресурсы  800 чел./час.

а) Определить оптимальный ассортимент, максимизирующий прибыль.

в) Количество столов и стульев относится как 1:6.

Задача о раскрое или минимизации обрезков.

Продукция бумажной фирмы выпускается в виде бумажных рулонов стандартной ширины – по 20 дм. По специальным заказам потребителей фирма поставляет рулоны и других размеров, для чего производится разрезание стандартных рулонов. Типичные заказы на рулоны нестандартных размеров приведены в таблице.

Специализированные заказы выполняются на разрезном устройстве, режущая кромка которого устанавливается в требуемом положении, причем рулон может быть разрезан несколькими способами.

Способ : кусок 7 дм, кусок 9 дм и остаток 4 дм

Способ : кусок 7 дм, кусок 5дм, кусок 5 дм и остаток 3дм

Способ : кусок 9 дм, кусок 5дм, кусок 5 дм и остаток 1дм

Чтобы выполнить поступившие заказы на рулоны нестандартной ширины (5, 7 и 9 дм), можно использовать различные сочетания вариантов разрезания, например,

1) разрезать 300 (стандартных рулонов) по варианту и 75 рулонов по варианту ;

2) разрезать 200 (стандартных рулонов) по варианту и 100 рулонов по варианту .

Какой из вариантов лучше? Качество каждого из вариантов можно оценить, сравнивая потери бумаги за счет обрезков. При первом способе потери бумаги составят дм, при втором способе дм. Дополнительные потери бумаги связаны с тем, что избыточные рулоны шириной 5, 7 и 9 дм также следует рассматривать как отходы производства. При первом способе вариант дает избыточных рулонов шириной 7 дм, а вариант избыточных рулонов той же ширины. Дополнительные потери составят дм. При втором способе не будет излишка рулонов 7 и 9 дм, но вариант даст избыточных рулонов шириной 5 дм. Дополнительные потери составят дм. В результате получаем, что суммарные отходы при первом способе составят

а при втором способе

Таким образом, второй способ лучше первого.

Общая постановка задачи: найти сочетание вариантов раскроя, при которых поступившие заказы удовлетворяются с минимальными потерями.

- количество стандартных рулонов, разрезаемых по варианту .

Количество рулонов шириной 5 дм ,

количество рулонов шириной 7 дм ,

количество рулонов шириной 9 дм .

Избыточное количество рулонов обозначим через , , соответственно. Тогда

Суммарная величина потерь выражается так:

Задача линейного программирования имеет вид:

Решение в MATHCADе.

Вопросы к экзамену по курсу Высшая математика (IV семестр)

(лектор – Борисова О.Н. )

1. Стандартная и каноническая формы представления задач линейного программирования. Геометрическая интерпретация задач линейного программирования.

2. Полные жордановы исключения. Преобразования систем линейных уравнений и неравенств методом полных жордановых исключений.

3. Симплекс-метод. Симплексные таблицы. Экономическая интерпретация элементов симплексной таблицы.

4. Двойственные задачи и методы. Экономическая интерпретация пары двойственных задач.

5. Экономическая и математическая формулировки транспортной задачи. Правила построения цепей. Потенциалы. Метод потенциалов. Основные способы построения начального опорного решения. Транспортные задачи с нарушенным балансом производства и потребления.

6. Антагонистическая игра двух лиц с нулевой суммой. Верхняя и нижняя цена игры. Седловая точка. Цена игры.

7. Чистые и смешанные стратегии игроков. Вероятностная интерпретация. Теорема о существовании решения игры в смешанных стратегиях. Графическое решение в случае игры 2n и n2 .

8. Сведение решения игры к задаче линейного программирования. Экономическая интерпретация игры с нулевой суммой.

9. Балансовые модели Леонтьева. Валовой, конечный, чистый продукт, внутрипроизводственное потребление. Матрицы прямых и полных производственных трат. Косвенные траты. Прямые и полные затраты труда и фондозатраты. Определение цены конечной продукции.

^ Типовой экзаменационный билет (письменный экзамен).

1. Математические модели межотраслевого баланса. Матрицы прямых и полных производственных трат. Косвенные траты. Валовой, конечный и чистый продукты. Прямые и полные затраты труда и фондозатраты. Определение цены конечной продукции.

2. Решить задачу линейного программирования z = 2x+y  max, x+y  5, x+2y  1, x  0, y  0.

3. Решить транспортную задачу: имеется три поставщика с ресурсами 100, 200, 300, три потребителя с потребностями 200, 150, 250, и матрица коэффициентов стоимости поставок . Определить план поставок наименьшей стоимости.

– «Формализованные методы принятия решений» – Решение задач принятия решений модифицированным симплексным методом Мебельная фабрика выпускает диваны

Задача 1.118. На мебельной фабрике изготовляется пять видов продукции: столы, шкафы, диваны-кровати, кресла-кровати и тахты.

На мебельной фабрике изготовляется пять видов продукции: столы, шкафы, диваны-кровати, кресла-кровати и тахты. Нормы затрат труда, а также древесины и ткани на производство единицы продукции данного вида приведены в табл. 1.53.

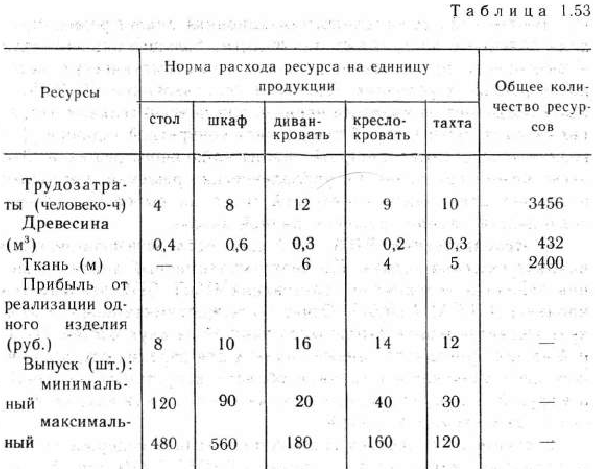
В этой же таблице указана прибыль от реализации одного изделия каждого вида, приведено общее количество ресурсов данного вида, имеющееся в распоряжении фабрики, а также указано (на основе изучения спроса), в пределах каких объемов может изготовляться каждый вид продукции.

Определить план производства продукции мебельной фабрикой, согласно которому прибыль от се реализации является максимальной. Используя ППП Л112, найти решение задачи, а также провести послеоптимизационный анализ полученного решения.

Решение:

Составим математическую модель задачи. Для этого предположим, что мебельная фабрика изготовит каждый из пяти видов продукции (стол, шкаф, диван-кровать, кресло-кровать и тахту) в количестве, соответственно равном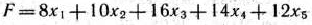

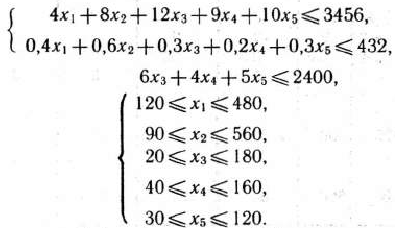
Значение целевой функции задачи (89) определяет величину прибыли, получаемую мебельной фабрикой при данном плане производства продукции, а выполнение неравенств (90) системы ограничений обеспечивает непревышение имеющихся в распоряжении фабрики ресурсов.

В соответствии с требованиями ППП ЛП2 каждой переменной, каждому неравенству системы ограничений (90) и целевой функции (89) присваиваем имена. Переменным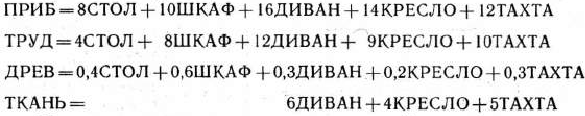

Используя последнюю систему уравнений, составляем матрицу исходных данных задачи (табл. 1.54).

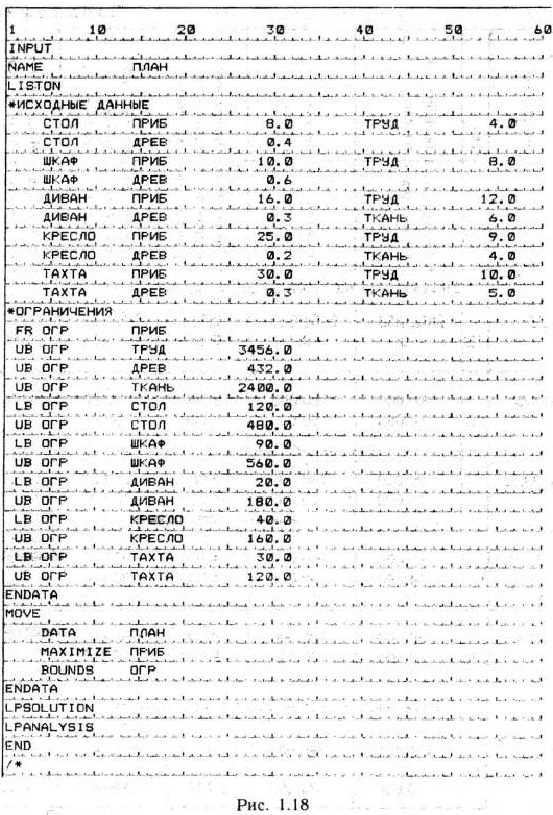
Исходные данные задачи, операторы управления и операторы описания записываем на специальном бланке (рис. 1.18), так же как мы это делали при нахождении решения задачи линейного программирования в § 1.5. Вместе с тем, чтобы получить отчет о послеоптнмизационном анализе решения задачи, после оператора LPSOLUTJON указываем оператор LPANALYSIS (ср. рис. 1.10 и 1.18).

После этого производим решение задачи на ЭВМ, Результаты решения выдаются в виде двух таблиц (см, табл. 1.55 и 1.56),

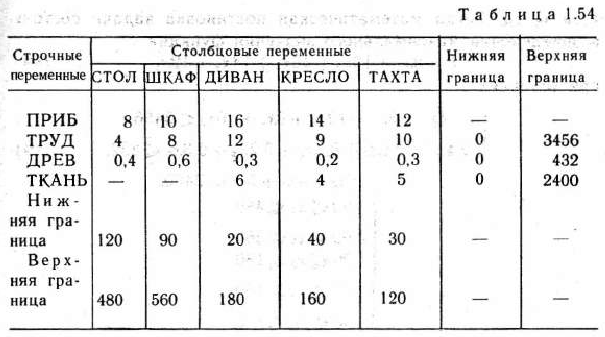
В табл. 1.55 содержится отчет о решении задачи (о чем было подробно сказано в § 1.5), а в табл. 1.56 — отчет о послеоптимиза-ционном анализе решения задачи.

Из табл. 1.55 видно, что оптимальным планом производства продукции мебельной фабрикой является план, согласно которому изготовляется 459 столов, 90 шкафов, 20 диванов-кроватей, 40 кресел-кроватей и тахты в количестве, равном 30. В соответствии с этим планом производства продукции прибыль фабрики от ее реализации является максимальной и равна 5812 руб., причем полностью используются трудовые ресурсы и остаются не использованными древесина и ткань.

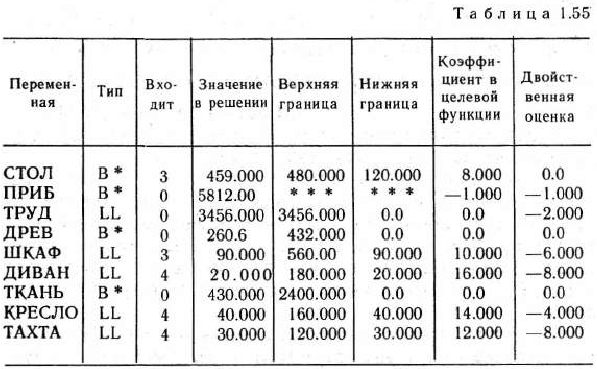
Проведем теперь анализ полученного решения задачи. Для этого воспользуемся данными та-бл. 1.56. Как видно, эта таблица состоит из двух частей. В первой части приводятся данные для анализа переменных, принявших свои значения на границе области их допустимых значений (переменные типа LL, UL и FQ), а во второй части — для переменных, принявших свои значения внутри области допустимых значений (переменные типа В*).

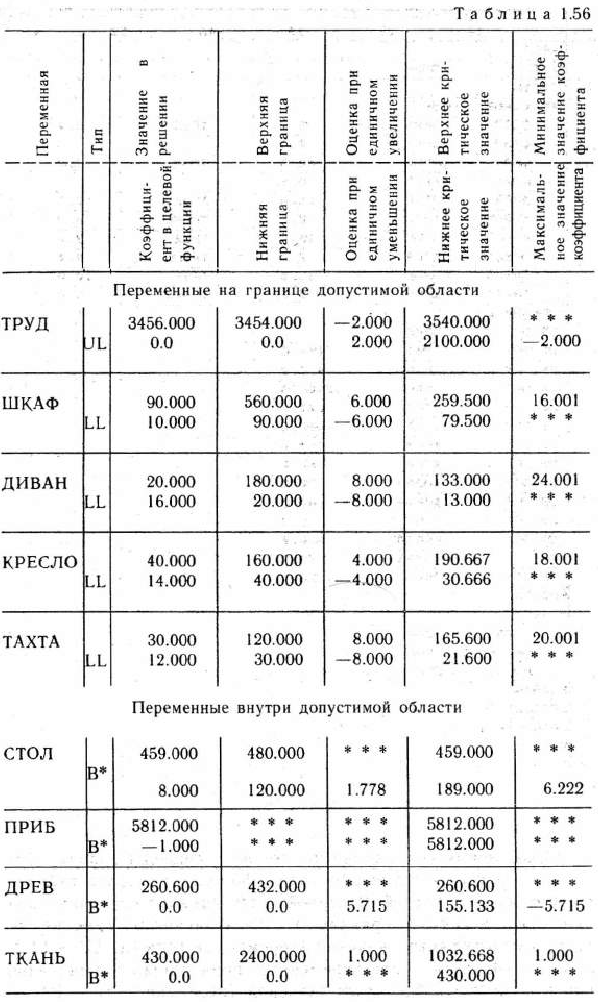
Первые четыре графы табл. 1.56 повторяют исходные данные и воспроизводят результат решения задачи.

В пятой графе указываются оценки, характеризующие степень изменения целевой функции при единичном изменении значения данной переменной (заметим, что знаки оценок соответствуют тому случаю, когда находится минимум целевой функции; в случае максимизации целевой функции, как в рассматриваемой задаче, знаки оценок следует изменить на противоположные). Действие оценок справедливо в интервале от нижнего до верхнего предельного значения переменной. Так, например, если принудительно увеличить выпуск диваиов-кроватей на один и довести до 21 (оптимальным планом производства продукции предусмотрено изготовление 20 диванов-кроватей), то это приведет к уменьшению прибыли мебельной фабрики на € руб.

Такое изменение прибыли будет иметь место при каждом увеличении выпуска на один диван-кровать до тех пор, пока выпуск данной продукции не превзойдет 133 шт.

Далее, если теперь рассмотрим один из видов ресурсов, например древесину, то видим, что этот вид ресурсов при оптимальном плане производства продукции используется не полностью. Вместе с тем если считать, что его объемы заключены между 260,6 и 155,133 м3, то каждое принудительное уменьшение объема использования данного ресурса на 1 м’1 приведет к уменьшению прибыли на 5,715 руб.

Рассмотрим теперь шестую графу табл. 1.56. В ней указываются пределы, в которых принудительно можно изменять значения переменных, так что базис, определяющий данный оптимальный план, остается неизменным. Так, например, если изготовле-. ние столов, выпуск которых в соответствии с оптимальным планом равен 459, изменять от 189 до 459, то базис, определяющий исходный оптимальный план, не меняется. Этот базис сохраняется и в том случае, если объем трудозатрат изменяется в пределах от 2100 до 3540 человеко-ч.

Рассмотрим, наконец, седьмую графу табл. 1.56. В ней указывается, в каких пределах могут изменяться значения коэффициентов целевой функции задачи, так что найденный оптимальный план остается неизменным. При этом в указанной графе табл. 1.56 приведены данные для того случая, когда находится минимум функции. В том случае, когда находится максимум функции (как в рассматриваемой задаче), в шестой графе верхние и нижние строки следует поменять местами. Так, например, для диванов-кроватей, прибыль от реализации которых равна 20 руб., максимальное значение коэффициента при переменной ДИВАН в целевой функции равно 24, а минимальное не ограничено. Это означает, что если прибыль от реализации одного дивана-кровати не превышает 24 руб., то выпускать диваны-кровати сверх установленного задания (20 шт.) невыгодно. Если прибыль окажется больше чем 24 руб., то выпуск диванов-кроватей при оптимальном плане производства продукции превысит 20 шт.

Из рассмотренного примера видно, что использование ППП ЛП2 позволяет не только найти решение задачи, но и провести довольно полный послеоптимизационный анализ полученного решения. Еще более полный послеоптимизационный анализ позволяет провести использование ППП ЛП АСУ.

Эта задача взята со страницы решения задач по предмету «математическое программирование»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Читайте также: